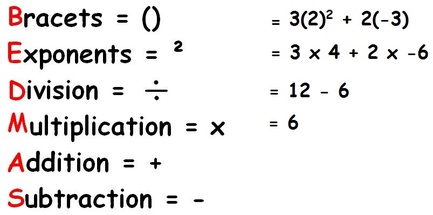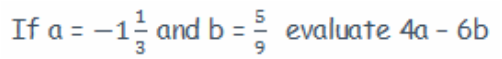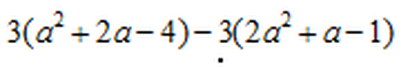TODAY'S AGENDA: Day 1-Course Intro/ Skills Review I
Great spirits have always encountered violent opposition from mediocre minds. Albert Einstein
|
1) Sit wherever you like; however seating arrangement will change monthly. :)
2) Let's brainstorm some classroom expectations. 3) Read MPM2D1 Course information 4) We will go through the lesson together as a class. 5) In pairs or independently, work on "Skills Review 1" Handout. LEARNING GOAL I will evaluate mathematical expressions and solve equations. |
HANDOUTS
|
| ||||||||||||
WARM UP
LESSON: Skills Review I
A. EVALUATING ALGEBRIC EXPRESSIONS
1. Substitute the given numbers in place of the variables. (variables: a, b, c, x, y, etc.)
2. Evaluate using the order of operations. (BEDMAS: Brackets, Exponents, Division, Multiplication, Addition, Subtraction)
Ex.1
YOUR TURN:
Ex.2
Ex.2
Ex.3 p=-3, evaluate 4p - 5 + 2p
Ex.4 Simplify
Ex.4 Simplify
B. SOLVING EQUATIONS
An equation contains an equal sign.
A solution is a value that makes the left side (LS) equal the right side (RS).
To solve an equation with one variable, isolate (leave alone) the variable.
Ex.1
x = 3 is the solution to 5x + 3 = 2(x+5) + 2 since
LS = RS.
Want to check? Well, let's sub 3 for "x" on each side.
LS= 5x + 3 RS = 2(x+5) + 2
= 5(3) + 3 = 2(3+5) + 2 = 15 + 3 = 2(8) + 2
= 18 = 16 + 2
= 18
YOUR TURN: Volunteers for the solutions.
Ex.2 Is x = 5 a solution for 2x - 4 = 5?
Ex.3 Solve 6x + 8 = 4x - 10
Ex.4 Solve 5(x + 2) = x + 6(x - 3)
Ex.5 Solve 1/2 (x - 1) = 1/4 (x + 1)
An equation contains an equal sign.
A solution is a value that makes the left side (LS) equal the right side (RS).
To solve an equation with one variable, isolate (leave alone) the variable.
Ex.1
x = 3 is the solution to 5x + 3 = 2(x+5) + 2 since
LS = RS.
Want to check? Well, let's sub 3 for "x" on each side.
LS= 5x + 3 RS = 2(x+5) + 2
= 5(3) + 3 = 2(3+5) + 2 = 15 + 3 = 2(8) + 2
= 18 = 16 + 2
= 18
YOUR TURN: Volunteers for the solutions.
Ex.2 Is x = 5 a solution for 2x - 4 = 5?
Ex.3 Solve 6x + 8 = 4x - 10
Ex.4 Solve 5(x + 2) = x + 6(x - 3)
Ex.5 Solve 1/2 (x - 1) = 1/4 (x + 1)