QUIZ ON TUESDAY... 

Day 4 - Function Notation, Domain & Range

TODAY'S AGENDA
SMILE because there is not enough space for happiness and sadness at the same time on our faces.

1) Review "Introduction to Functions Worksheet" VLT
2) WARM UP: The video 
3) LESSON: 1.2 Function Notation, 1.4 Domain & Range
4) HW: Complete the handouts


LEARNING GOAL
I will use proper notation for writing functions, domain, and range.

HANDOUTS

Day 3 - Function Notation, Domain & Range HANDOUT
File Size: 190 kb
File Type: doc
Download File

WARM UP

LESSON: 1.2 Function Notation

It is useful to give a function a name.
The most common name is "f", but we can have other names like "g", "h", etc.

But let's use "f":
Picture
Copied from www.mathisfun.com
To evaluate f(a), substitute a for "x" in the equation for f(x).

Example: f(x) = 5x + 2 

a) f(3) = 5(3) + 2 = 15 + 2 = 17

b) f(4a + 1) = 5(4a + 1) + 2
                    = 20a + 5 + 2
                    = 20a + 7


YOUR TURN
g(x) = 2x^2 - 3x + 1 (Read: 2x squared minus 3x plus 1)


a) g(1) = ?                          b) g(-1) = ?                   c) g(2a-1) = ? 

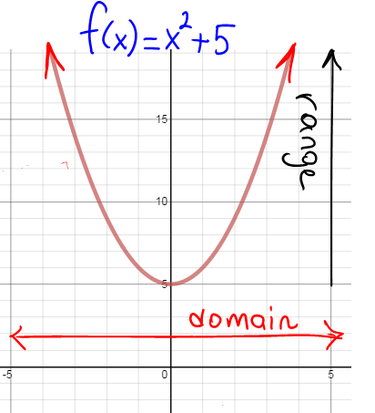
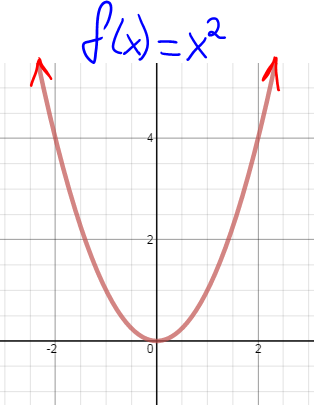
LESSON: 1.4 Domain and Range

Domain: The domain is all the values that go into function. In other words, the possible values of x (input values).

How to state Domain
D: {x|x∈R} 
It means  x such that x can be any value in the Real numbers.
"∈" is the symbol meaning "in the set of"

Range: The range is all the values that come out. In other words, the possible values of y (output values).

How to state Range
R: {y|y≥5, y∈R} 
It means y such that y is greater than or equal to 5, where y is a Real number.


Example 1
- State the domain and range of the following relation: (eye color, student's name).
- State whether the relation is a function.

A = {(blue,Jacob),(green,Luke),(brown,Parsa),(blue,Sunna),(brown,Jack),(green, Riju)}

Solution

D:{blue, green,brown}
R:{Jacob, Luke, Parsa, Sunna, Jack, Riju}
This is not a function because the eye colours are repeated.


Example 2
- State the domain and range of the following relation: 
- State whether the relation is a function.

 {(1,3), (-2,7), (3,-3), (4,5), (1,-3)}

Solution

Domain: {-2, 1, 3, 4}.
Range: {-3, 3, 5, 7}.
While these listings appear in ascending order, ordering is not required. Do not, however, duplicate an element.
No, this relation is not a function. The x-value of "1" had two corresponding y-values (3 and -3).



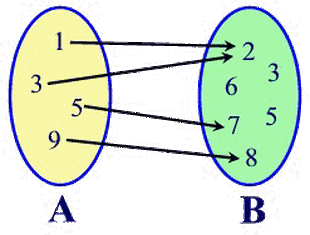
Example 3
State the domain and range for the elements matched in the diagram below.
State whether the matches form a function.

Solution

Domain: {1, 3, 5, 9}.
Range: {2, 7, 8}.
Yes, the relation {(1,2), (3,2), (5,7), (9,8)}is a function. No x-value repeats..


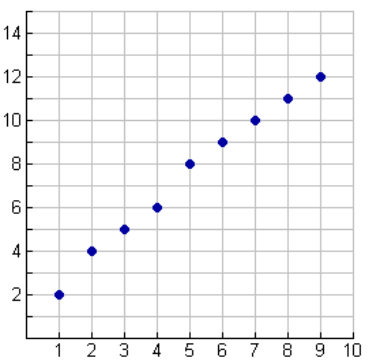
Example 4
State the domain and range associated with the scatter plot shown below.
State whether the scatter plot is a function.

Solution

Domain: {1,2,3,4, 5, 6, 7, 8, 9}.
Range: {2, 4, 5, 6, 8, 9, 10, 11, 12}.
Yes, this is a function. No x-values repeat, and it passes the Vertical Line Test for functions.


Example 5
State the domain and range associated with the scatter plot shown below.
State whether the scatter plot is a function.

Solution

Domain: {x|x∈R} x such that x is an element of real numbers.
Range: {y|y≥0, y∈R} y such that y is greater than or equal to 0 and an element of real numbers.
Yes, this relation is a function, since it passes the Vertical Line Test for functions.


SOLUTIONS: It's a slideshow. Click the top of the page to navigate.